11. Mass and Center of Mass

a. Mass

1. Bar with Non-Uniform Density

If a bar of metal has length \(L=5\,\text{cm}\) and its mass is \(M=35\,\text{gm}\) then its linear density is \(\displaystyle \delta=\dfrac{M}{L} =\dfrac{35\,\text{gm}}{5\,\text{cm}}=7\,\dfrac{\text{gm}}{\text{cm}}\) provided the mass is uniformly distributed over the bar.

We call this linear density because it has units of mass per unit length whereas the more familiar volume density has units of mass per unit volume. Later, we will also consider surface density whose units are mass per unit area. When the context is clear, the word density may be used to mean any of these three quantities.

Conversely, if the mass is uniformly distributed over a bar of length \(L=12\,\text{cm}\) and the density is \(\delta=4\,\dfrac{\text{gm}}{\text{cm}}\), then the total mass is: \[ M=\delta L=4\,\dfrac{\text{gm}}{\text{cm}}\times12\,\text{cm} =48\,\text{gm} \]

You can tell that you multiply the density and the length to get the mass because the \(\text{cm}\) units cancel leaving the units of \(\text{gm}\): \[ M=\delta L=4\,\dfrac{\text{gm}}{\cancel{\text{cm}}}\times12\,\cancel{\text{cm}} =48\,\text{gm} \]

On this page, we consider the situation when the mass is not uniformly distributed over the bar, i.e. when the linear density \(\delta(x)\) is a function of the position \(x\) along the bar.

Find the total mass of a bar between \(x=a\) and \(x=b\) whose linear density is \(\delta(x)\).

We first cut up the bar into \(n\) small pieces each of width \(\Delta x=\displaystyle \dfrac{b-a}{n}\).

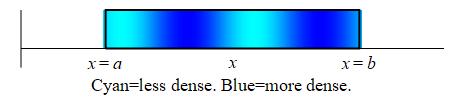
The plot shows a bar from x equals a to b, with uneven density
which alternates between two colors.

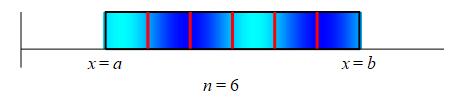
The plot starts with the same plot as above, and adds 5 vertical lines
which separate the bar into 6 small rectangles equally. Below the plot
there is a caption which says n equals 6.

Since the density is not constant, we approximate the density of the \(i^\text{th}\) piece as \(\delta(x_i^*)\) where \(x_i^*\) is a point in the \(i^\text{th}\) region. Then the mass of the \(i^\text{th}\) region is approximately \(m_i\approx\delta(x_i^*)\Delta x\). As the length of each piece gets smaller, the approximation gets better. The total mass is then obtained by adding up the masses of the small pieces and taking the limit as the number of pieces becomes large, (\(n\to\infty\)) and hence the length of each piece gets small (\(\Delta x\to0\)): \[ M=\lim_{n\to\infty}\sum_{i=1}^n m_i =\lim_{n\to \infty}\sum_{i=1}^n\delta(x_i^*)\Delta x \] This limit of a sum is recognized as the integral \(\displaystyle \int_a^b \delta(x)\,dx\).

The total mass of a bar with linear density \(\delta(x)\) between \(x=a\) and \(x=b\) is: \[ M=\int_a^b \delta(x)\,dx \]

Find the total mass of an \(8\,\text{m}\) bar whose linear density is \(\delta(x)=(1+x)\dfrac{\text{kg}}{\text{m}}\) if \(x\) is measured from one end.

The plot shows a bar from x equals 0 to 8, which is shaded from light
on the left to dark on the right, showing it is with more dense close
to x equals 8.

The total mass is \[\begin{aligned} M&=\int_0^8 \delta(x)\,dx =\int_0^8 (1+x)\,dx \\ &=\left[x+\dfrac{x^2}{2}\right]_{x=0}^8 =8+\dfrac{64}{2}=40\,\text{kg} \end{aligned}\]

Your turn:

Find the total weight (in \(\text{lbs}\)) of a \(10\,\text{ft}\) bar whose linear weight density is \(\delta(x)=\dfrac{1}{1+x}\dfrac{\text{lb}}{\text{ft}}\) if \(x\) is measured from one end.

The plot shows a bar from x equals 0 to 10, which is shaded from
dark on the left and light on the right, showing it is more dense
close to x equals 0.

Note: If we are given a weight density instead of a mass density, then we use the letter \(W\) for the total weight instead of \(M\) for the total mass.

\(W=\ln(11)\,\text{lb}\)

\[\begin{aligned} W&=\int_0^{10} \dfrac{1}{1+x}\,dx =\left.\ln(1+x)\right|_0^{10} \\ &=\ln(11)-\ln(1)=\ln(11)\,\text{lb} \end{aligned}\]

11. Mass and Center of Mass

a. Mass

1. Bar with Non-Uniform Density

Heading